【进阶算法】欧拉图中的欧拉通路和欧拉回路问题

力扣上的两道欧拉图问题：

• 332. 重新安排行程
• 753. 破解保险箱

前置知识

• 欧拉通路：不重复经过同一条边的前提下，遍历完图的全部结点。
• 欧拉回路：不重复经过同一条边的前提下，遍历完图的全部结点的一条环路。
• 欧拉图：存在欧拉回路的连通图。
• 半欧拉图：存在欧拉通路但不存在欧拉回路的连通图。
• 有向图存在欧拉通路的充要条件：图连通且每一个结点的入度和出度都相同。

例题 1：重新安排行程

找欧拉通路。

构造欧拉图

根据 tickets 构造欧拉有向图，然后在给定的图中搜索一条字典序最小的欧拉通路。

代码

/**
 * @param {string[][]} tickets
 * @return {string[]}
 */
var findItinerary = function(tickets) {
    const heaps = new Map();
    // 构造欧拉邻接图，图的数据结构为哈希表
    // (key, heap), heap 存放所有能从起点 key 直接飞抵的下一站
    // heap 按照字典序升序
    for (const [src, dst] of tickets){
        if (!heaps.has(src)){
            heaps.set(src, new Heap((a, b) => {
                if (a > b) return 1;
                else if (a < b) return -1;
                else return 0;
            }));
        }
        heaps.get(src).insert(dst);
    }
    const ans = [];
    const dfs = curr => {
        // 还没遍历完所有分支 且 当前 curr 非死胡同分支
        while (heaps.has(curr) && heaps.get(curr).size > 0){
            // 贪心地选择 curr 的下一站中字典序最小的，保证最终答案的字典序
            dfs(heaps.get(curr).removeTop());
        }
        // 入栈条件：当 curr 的所有下一站都去过后（出度减为 0），curr 变为死胡同点，说明
        // curr 为当前航线路径的【终点】
        // 因此，ans 实际上保存的是从终点到起点的倒序路径
        ans.push(curr);
    }
    dfs("JFK"); // 起点按照题目要求，设置为 JFK
    return ans.reverse();
};

class Heap {/* 堆的代码略 */}

例题 2：破解保险箱

找欧拉回路。

题目释疑

本题的题目和示例都有些令人费解。如何理解示例 2？

首先说疑问，为什么答案不是 00 或 01 或 10 或 11？

因为题目要求能打开保险箱的最短字符串，准确说是确保一定能打开保险箱的最短字符串。00/01/10/11 都只是密码的其中一种可能，答案字符串应当包含密码的所有可能子串。也就是说，答案字符串应当是 00/01/10/11 的公共父串。

以示例 2 的答案 00110 为例。首先 00110 前两个数字 00 ，包含了 00； 然后加上第三个数字 1，001，包含了 01；然后输入数字 1，得到 0011，包含 11；最后是数字 0，得到 00110，包含 10。00110 完美囊括四个可能密码。

对「最短」的理解：每输入一个新数字都对应一个新的答案子串。

构造欧拉图

此题对应的欧拉图如何构造？

假设 n 位密码，k 进制数字，则对应的欧拉图：

• 总共 k^n-1 个结点，每个结点代表一个 n-1 bits 的数字
  • k^n-1 怎么来的？n-1 位数字，每位数字是一个 k 进制数，总共有 k * k * … * k （n-1 个 k 连乘）种可能。
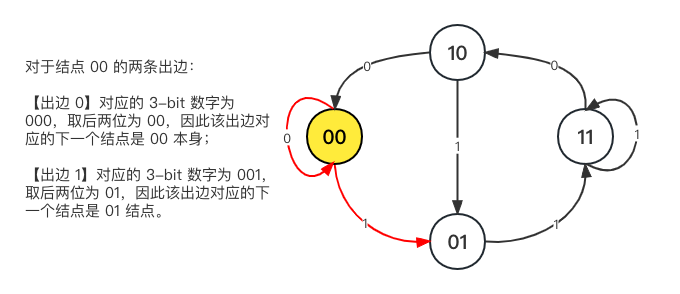
• 每个结点对应 k 条出边和 k 条入边，第 i 条出边代表输入的下一位数字等于 i
• 结点 + 某条出边代表一个 n bits 的数字

e.g. 结点 node 代表 n-1 bits 数字 a₁a₂…a_n-1，它的其中一条出边 x 连接的 n-1 bits 数字为 a₂a₃…a_n-2x，node 和出边 x 组合起来代表的 n bits 数字是 a₁a₂…a_n-1x。

此题的欧拉图不需要像上一题那样提前构造，在 dfs 过程中动态构造就 ok。

代码

/**
 * @param {number} n
 * @param {number} k
 * @return {string}
 */
var crackSafe = function(n, k) {
    // 本题可抽象为有向图，有向图存在欧拉回路的充要条件：
    // 一个有向图存在欧拉回路，所有顶点的入度等于出度且该图是连通图。

    let highest = Math.pow(10, n-1); // k 的 max value = 10
    // n-1 位 k 进制数必定小于 highest
    let ans = '';
    const seen = new Set(); // 已经经过的答案子串
    const dfs = node => {
        // x -> [0, k-1], 每一条出边都去一次
        for (let x = 0; x < k; x++){
            // next 为 node 和其出边 x 对应的【n 位数字】的值
            // 当前 node 左移一位，因为是十进制所以乘以 10
            let next = node * 10 + x;
            // 题目要求【最短】
            // 也就是每一个节点都必须对应一个新的答案子串，不能重复经过同一个答案子串
            if (!seen.has(next)){
                seen.add(next);
                // 取后 n-1 位，继续搜索
                // next % highest 代表的出边就是 node 的 x 出边连接的下一个节点代表的 n-1 位数字
                dfs(next % highest);
                ans += x;
            }
        }
    }
    dfs(0);
    // '0'.repeat(n-1) 是初始的 n-1 位数字
    // 对应的就是 dfs(0)，从 0 开始
    ans += '0'.repeat(n-1);
    return ans;
};