【进阶算法】Morris 中序遍历

Morris 中序遍历

例题：剑指 Offer II 054. 所有大于等于节点的值之和

本例题是反序中序遍历（即下面引文中的“左”<->“右”要反着看），其官解是这样解释 Morris 遍历的：

Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其反序中序遍历规则总结如下：

• 如果当前节点的右子节点为空，处理当前节点，并遍历当前节点的左子节点；
• 如果当前节点的右子节点不为空，找到当前节点右子树的最左节点（该节点为当前节点中序遍历的前驱节点）；
  • 如果最左节点的左指针为空，将最左节点的左指针指向当前节点，遍历当前节点的右子节点；
  • 如果最左节点的左指针不为空，将最左节点的左指针重新置为空（恢复树的原状），处理当前节点，并将当前节点置为其左节点；
• 重复步骤 1 和步骤 2，直到遍历结束。

我的疑问在这句：“如果最左节点的左指针不为空，将最左节点的左指针重新置为空（恢复树的原状）”，既然已经是「最左结点」了，怎么可能左指针不为空呢？最左结点的左指针难道不是必然为空吗？否则怎么会成为最左呢？

看这个油管视频搞懂了：最左结点还有左指针的情况，是在上一步“如果最左节点的左指针为空，将最左节点的左指针指向当前节点”的时候将结点与其后继结点连接在一起时做的特殊处理（i.e. 下图虚线的箭头指针），正是这个特殊处理使得 Morris 遍历无需依靠栈就能从左子树回到根结点。

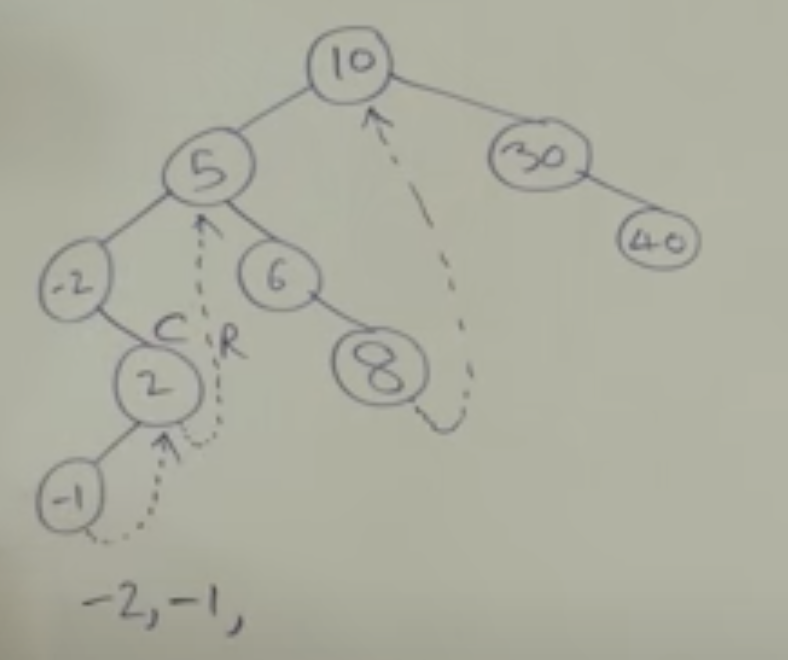上图的虚线箭头就是临时连接的右指针，8 -> 10 代表 10 是 8 的后继结点（在中序遍历序列中 10 正是 8 的下一位）

思想

中序遍历的顺序为：左 -> 根 -> 右。在脑海中想象从树的根节点开始移动遍历指针会发现，我们可以通过 root = root.left 以及 root = root.right 方便地从根结点转移到左子树或者右子树，但没办法通过结点上的某个指针回到结点的父结点（因为没有 root.parent 这样指向父结点的指针）。

于是，由于这个特性（有办法直接从父到子，但没有直接方法从子到父），中序遍历代码实现的核心在于：当遍历完左子树之后，如何回到其根节点？

递归的返回方法简单粗暴，一边由父下降到子，一边在内存栈中存父结点（碰到一个存一个）。等到子结点处理完后，按序弹出栈内的结点再处理就好；

迭代的方法也是依靠栈。先把根节点全部存在栈（代码写的栈）中，待其左子树全部遍历完毕后，再出栈处理。

以上两种方法都是利用了栈的特性间接从左子树回到根结点。

Morris 遍历的独特与核心实现就在回到根结点的方法上。它没有使用额外的栈，而是利用树本身的空闲子结点指针记录后继结点，为遍历指针临时连接回头路：

• 利用左子树最右结点空闲的右指针（最右必定 root.right == null，且最右结点必定是根结点的前驱结点），将当前结点（左子树最右结点）与其后继结点（根结点）连接起来，方便之后指针从左子树回到根结点
• 再次遍历到这个最右结点时，再把这个连接断掉，恢复树的原状

代码及注释

测试地址：94. 二叉树的中序遍历

var inorderTraversal = function(root) {
    let curr = root;
    const ans = [];
    while (curr){
        // is leftmost node?
        if (!curr.left){ // yes
            // 左子树为空
            ans.push(curr.val); // 则处理根结点
            curr = curr.right; // 根结点处理完毕后转到右子树
        }else{ // no
            // succ 为 curr 的左子树的最右结点，即 curr 的前驱结点；
            // 反之 succ 为 curr 的后继结点
            let succ = getSuccessor(curr);
            // 众所周知，二叉树的遍历过程中，每一个结点会被经过 3 次
            // if 为第一次经过结点 curr 时（正在沿路下降到左子树）的处理
            // else 为第二次经过结点 curr 时（左子树处理完毕回到根结点）的处理
            // （迭代的方法无法捕捉到第三次，不过不重要，这里不需要捕捉第三次经过结点）
            if (!succ.right){ // succ.right···>curr 这条线还没连上
                // 在根结点下到左子树结点过程中，一路连接沿路各根结点与其前驱结点
                succ.right = curr; // link the way back
                curr = curr.left; // continue going down the left child-tree
            }else{ 
                // succ.right···>curr 已连上，且已利用这条线从左子树回到根结点 curr
                succ.right = null; // break the link
                ans.push(curr.val); // curr 的左子树已遍历完，该处理 curr（根结点）了
                curr = curr.right; // 上一句处理完根结点，本句转移到右子树
            }
        }
    }
    return ans;
};
// 为什么需要连接前驱结点？因为中序遍历是先从根结点下降到左子树，
// 处理完左子树全部结点后需要返回根结点，连接前驱结点就是连通这条原路返回的路径
// 结点 node 的前驱结点就是中序遍历序列中，恰好排在 node 前一位
// 即结点 node 的左子树中的最右结点
// getSuccessor(node) return node's left tree's rightmost node
var getSuccessor = function(node){
    let succ = node.left;
    // 为什么需要 succ.right !== node?
    // 因为此函数会在连接好前驱结点后【再次】遍历到该结点
    // 此时由于前一次遍历，succ 的 right 临时连接到了 node，在树中形成一个临时的环
    // 如果不加上这个条件，将会陷入死循环
    while (succ.right && succ.right !== node) succ = succ.right;
    // 临时连接这里不着急断掉，主函数负责切断连接，此函数只负责返回前驱结点
    return succ;
}

Morris 代码最容易出错的点在 getSuccessor(node) 中的 while 循环条件：务必记得 succ.right !== node 这个循环条件，关键中的关键，否则会导致死循环。