将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后，数列就变成一个有序序列。
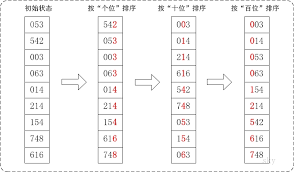LSD 示意图
基数排序的方式可以采用LSD（Least significant digital）或MSD（Most significant digital），LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。
LSD基数排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 获得数字num从右往左的第digit位
// 比如个位，digit=1；十位，digit=2
function getDigit(num, digit) {
num = Math.floor(num / Math.pow(10, digit - 1));
return num % 10;
}
function radixSortLSD(nums) {
// get the max bit number
const max = Math.max(...nums),
len = nums.length;
const maxBits = max.toString().length;
// 进行maxBits轮比较
for (let i = 1; i <= maxBits; i++) {
const bucket = {}; // Object会自动根据key的大小排升序
// 第i轮遍历数组，根据num的第i位排序
for (let j = 0; j < len; j++) {
// 获得当前元素的第i位数字
let radix = this.getDigit(nums[j], i);
if (!bucket[radix]) bucket[radix] = [];
bucket[radix].push(nums[j]); // 放在对应的桶内
}
nums = []; // 清空原数组
// 根据桶内元素排序重排nums数组
for (let key in bucket) {
nums = nums.concat(bucket[key]);
}
}
return nums;
}
假设n为nums.length，k为maxBits，即数组中位数最大值，决定了会进行几轮的放桶操作，r为有几种数字/字母
- 时间复杂度：o((n+r)*k)，每轮最后需重排组合
nums时，花费o(r) - 空间复杂度：o(n+r)
- 稳定性：稳定。因为相同元素始终会被放在同一个桶中，而两者的相对位置始终维持最开始的位置不变，因为插入顺序始终保持最初的相对顺序。
MSD基数排序
比LSD基数排序更优，MSD基数排序只会在最坏情况遍历数字的所有数位。
错误代码
直觉想法是：将LSD的流程反着来，从最高数位排序，数位不足maxBits的getDigit()会返回0
e.g.
getDigit(12, 3)，由于数字12没有百分位，12 // (10^2) % 10 = 0，所以可以直接沿用LSD的getDigit()。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function radixSort1(nums) {
// get the max bit number
const max = Math.max(...nums),
len = nums.length;
const maxBits = max.toString().length;
// 进行maxBits轮比较
for (let i = maxBits; i > 0; i--) {
// 放桶
const bucket = {}; // Object会自动根据key的大小排升序
// 第i轮遍历数组，根据num的第i位排序
for (let j = 0; j < len; j++) {
let radix = this.getDigit(nums[j], i);
if (!bucket[radix]) bucket[radix] = [];
bucket[radix].push(nums[j]);
}
nums = [];
// 根据桶内元素排序重排nums数组
for (let key in bucket) {
nums = nums.concat(bucket[key]);
}
}
return nums;
}
以上代码正确吗？
测试用例：[2, 34, 1, 6, 3, 10, 9, 2, 3, 7, 21, 95]
测试结果：错误
1
2
3
Wrong!
Submit: 10,1,21,2,2,3,3,34,95,6,7,9
Expect: 1,2,2,3,3,6,7,9,10,21,34,95
调试发现：
1
2
10分位排序后: 2,1,6,3,9,2,3,7,10,21,34,95
1分位排序后: 10,1,21,2,2,3,3,34,95,6,7,9
第一轮按照十分位排序，结果看起来没毛病：个位数都排在了前面（因为它们十分位都是0），两位数都在后面，并且两位数是按照升序排列好了；
问题出在第二轮。
第二轮结果就是最终结果，即 10,1,21,2,2,3,3,34,95,6,7,9。仔细一看它确实是按照个位排序的，只看个位就是 0,1,1,2,2,3,3,4,5,6,7,9。
正确代码
正确的想法应该是：高位数字排序好后，接下来分别对拥有相同高位的元素们进行排序，即原数组每经历一轮排序，就根据其高位数字被划分为几个子数组，然后子数组内部再进行下一轮排序，直到所有子数组内部均有序为止。
由下图可以看到，排序过程中很可能不会遍历到元素的所有数位，就能够排序完成，这是MSD排序优于LSD的关键。MSD基数排序的最佳状况是在第一轮排序最高位时就完成数组排序，此时只需要花费o(n + r)的时间。
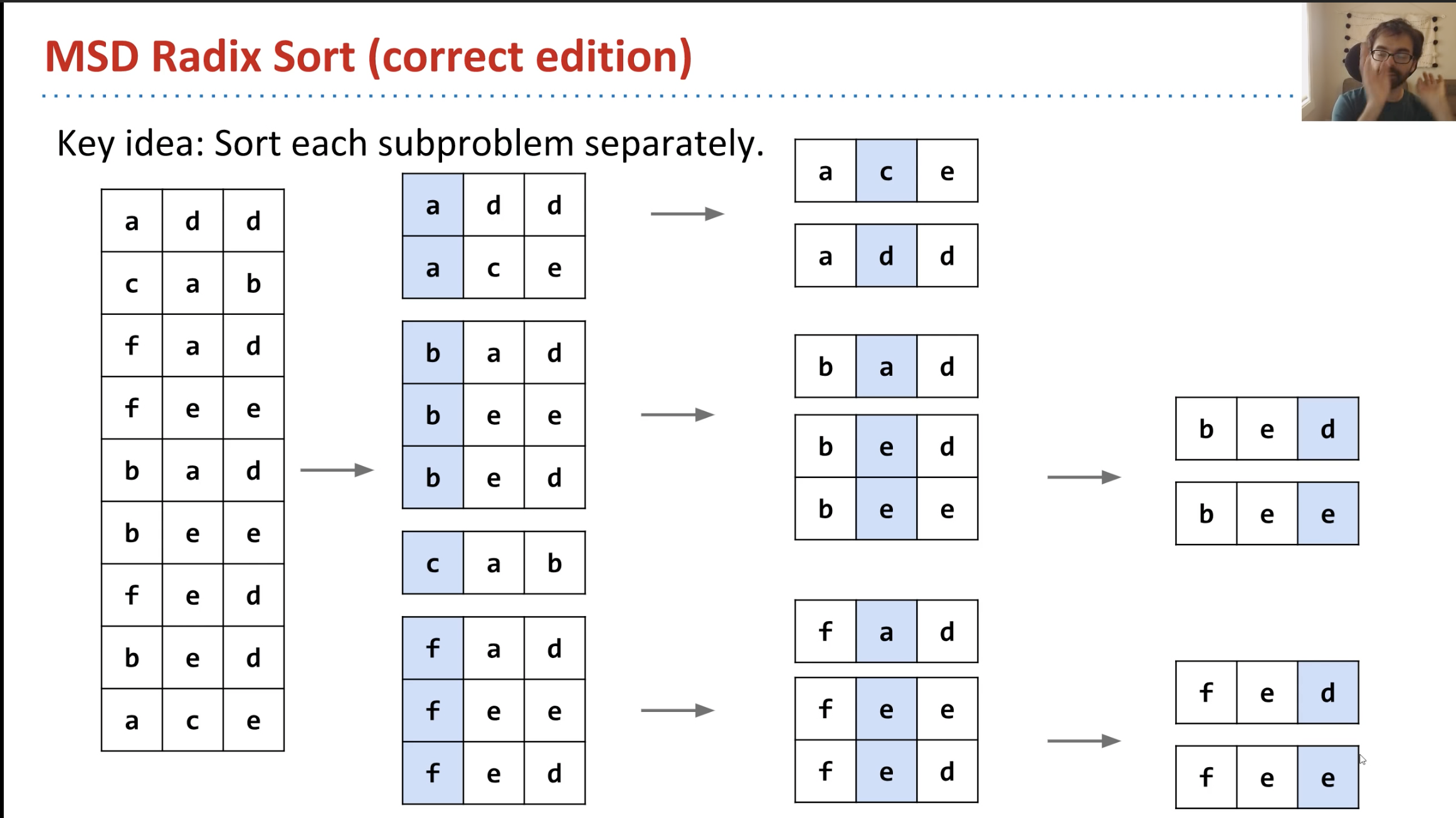MSD示意图，截取自参考视频
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function radixSortMSD(nums) {
// get the max bit number
const max = Math.max(...nums);
const maxBits = max.toString().length;
// 递归
const recur = (nums, digit) => {
if (digit <= 0) return nums;
const len = nums.length;
// 只剩下一个元素，直接返回
if (len <= 1) return nums;
// 放桶
const bucket = {}; // Object会自动根据key的大小排升序
// 第i轮遍历数组，根据num的第digit位排序
for (let i = 0; i < len; i++) {
let radix = this.getDigit(nums[i], digit);
if (!bucket[radix]) bucket[radix] = [];
bucket[radix].push(nums[i]);
}
nums = [];
// 每个桶内部分别进行排序，递归
for (let key in bucket) {
nums = nums.concat(recur(bucket[key], digit - 1));
}
return nums;
};
return recur(nums, maxBits);
}
假设n为nums.length，k为maxBits，即数组中位数最大值，决定了会进行几轮的放桶操作，r为有几种数字/字母
- 时间复杂度：最好o(n + r)，最坏o((n + r) * k)，每轮最后需重排组合
nums时，花费o(r) - 空间复杂度：o(n + k * r)，MSD基数排序使用递归，因此会比LSD费更多内存
- 稳定性：稳定